De Belgische wiskundige Sam Mattheus heeft een decenniaoud wiskundig probleem opgelost. ‘Ik had de impact van het oplossen van dit probleem onderschat.’
Het vraagstuk dat Sam Mattheus van de Vrije Universiteit Brussel (VUB) oploste, gaat over de zogeheten Ramseygetallen. Deze getallen geven aan hoe groot een netwerk kan worden voordat er onvermijdelijk patronen of structuren in ontstaan.
Het is erg moeilijk om Ramseygetallen te berekenen. Er zijn maar een paar oplossingen bekend. Bij het Ramseyprobleem dat Mattheus oploste, was de afgelopen veertig jaar geen vooruitgang geboekt. Mattheus werkte samen met wiskundige Jacques Verstraete van de Universiteit van Californië – San Diego, om daar verandering in te brengen.
Dit is hoe we wiskundefobie te lijf kunnen gaan
Sarah Hart vertelt hoe we de angst voor getallen en formules weg kunnen nemen.
De nieuwe methode die de twee wiskundigen ontwikkelden, loste niet alleen dit decenniaoude probleem op. Het biedt ook een nieuwe manier om andere Ramseyproblemen, uit de overkoepelende Ramseytheorie, aan te pakken.
Netwerken
De Ramseytheorie gaat over het ontstaan van structuren of patronen in wanorde. Mattheus keek naar zogeheten grafen. Dat zijn een soort netwerken die je kunt voorstellen als punten die onderling verbonden zijn. Het idee is dat er in grote netwerken – of grafen – altijd zekere structuren te vinden zijn.
Dit kun je je voorstellen aan de hand van de sociale netwerken, zoals die van Facebook. Binnen zo’n netwerk heb je groepen mensen die onderling bevriend zijn en groepen mensen die geen vrienden zijn. De Ramseyproblemen gaan over de volgende vraag: stel je wilt een groep vinden van tien mensen die ofwel allemaal onderling bevriend zijn, ofwel allemaal geen vrienden van elkaar zijn. Hoe groot moet je netwerk minimaal zijn om gegarandeerd zo’n groep te vinden? Oftewel: hoe groot moet het netwerk zijn dat die structuur erin opduikt?
Er zijn een paar Ramseyproblemen waarvoor een oplossing bestaat. Wil je bijvoorbeeld een groep vinden van drie vrienden óf drie niet-bevriende mensen? Dan lukt dat gegarandeerd als je zes willekeurige personen uitkiest. Kies je er slechts vijf, dan vervalt die garantie.
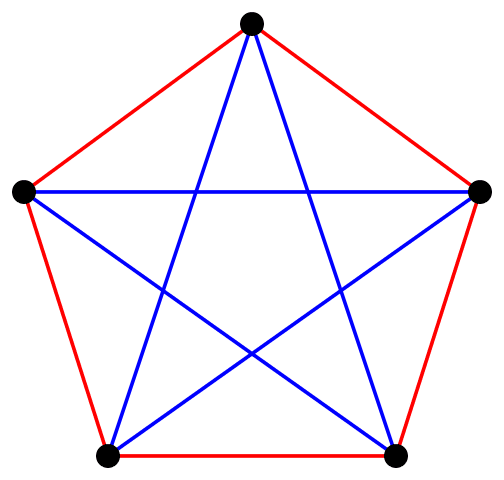
Wiskundig kun je Ramseygetallen van deze problemen schrijven als r(s,t), waarbij s het aantal onderling bevriende mensen is en t het aantal niet bevriende mensen. Het hierboven beschreven geval schrijf je dan als r(3,3) = 6.
Mattheus keek wat er met het Ramseygetal gebeurt als je een groepje van vier vrienden zoekt of groepje van een variërend aantal niet-bevrienden. Wiskundig is dat: r(4,t).
Missende ingrediënten
Mattheus vertrok vorig jaar, nadat hij gepromoveerd was aan de VUB, naar de Verenigde Staten om onder leiding van Verstraete aan Ramseygetallen te werken. ‘Ik was een paar jaar eerder een artikel tegengekomen van Verstraete en een collega waarin ze een nieuwe methode hiervoor beschreven’, zegt hij. Die methode was totaal verschillend van de pogingen daarvoor.
Verstraete en zijn collega hadden een recept gevonden waarmee ze Ramseyproblemen konden gaan oplossen. ‘Maar het probleem was dat de ingrediënten voor dat recept hopeloos zoek waren’, zegt Mattheus. Met de eindige meetkunde, het vakgebied waarin Mattheus promoveerde, kon er gezocht worden naar die ingrediënten.
Dankzij zijn kennis van de eindige meetkunde, vond Mattheus eerder dit jaar een bestaande graaf die hem interessant leek voor de Ramseyproblemen. Hij liep met dat idee het kantoor van Verstraete binnen en ze gingen ermee aan de slag. Slechts enkele maanden later leverde dit de oplossing op voor het Ramseyprobleem r(4,t).
Naïef
Het vinden van de graaf was voor Mattheus geen eurekamoment. ‘We hebben het nog flink moeten masseren om eruit te krijgen wat we wilden’, zegt hij. ‘En terwijl we eraan werkten was het op geen enkel moment duidelijk dat het zou gaan lukken.’
Pas nadat ze hun resultaat online gepubliceerd hadden en de interesse groot bleek, ontdekte Mattheus hoe belangrijk het probleem was waar hij aan had gewerkt. ‘Omdat ik geen achtergrond heb in de Ramseytheorie, had ik de impact van de oplossing onderschat’, zegt hij. ‘Misschien heeft mijn onwetendheid ook wel in mijn voordeel gewerkt. Als je niet weet hoe lang iets al een open probleem is en hoeveel goede wiskundigen er al aan hebben gewerkt, dan ben je namelijk nog naïef genoeg om iets te proberen. In dit geval iets dat bleek te werken.’
