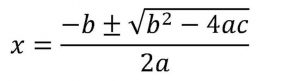De meeste mensen leren hem op de middelbare school uit hun hoofd en vergeten hem daarna zo snel mogelijk weer: de abc-formule. Een Amerikaanse wiskundige heeft nu een eenvoudigere en inzichtelijke methode ontwikkeld om deze formule af te leiden.
De abc-formule heeft betrekking op kwadratische vergelijkingen van de vorm y = ax2 + bx + c. Als je van zo’n vergelijking een grafiek maakt, levert dat een parabool op. Hierbij zijn a, b en c bekende getallen. Er zijn oneindig veel combinaties van a, b en c mogelijk en dus ook oneindig veel sommen die wiskundedocenten kunnen bedenken voor hun leerlingen.
Heino Falcke fotografeerde als eerste een zwart gat: ‘Nog mooier dan ik al die tijd had verwacht’
Heino Falcke, hoogleraar radioastronomie, maakte in 2019 de eerste foto van een zwart gat. Op dit moment doet hij onderzoek n ...
Nu gebruiken de meeste mensen die de middelbare school achter zich hebben gelaten kwadratische vergelijkingen niet dagelijks, maar ze hebben wel degelijk toepassingen. In de economie kun je ze gebruiken om de optimale prijs voor je product te bepalen. En in de natuurkunde en de lucht- en ruimtevaart komen diverse toepassingen van parabolen voor. Denk bijvoorbeeld aan de paraboolvormige baan van een bal die je omhoog gooit en die daarna weer valt.
Om de punten te vinden waar zo’n parabool de x-as snijdt, maken scholieren nu meestal gebruik van de abc-formule. Dat is een niet erg inzichtelijke methode, waarbij ze trucjes uit hun hoofd moeten leren en getallen moeten gokken. De nieuwe methode is inzichtelijker, bevat geen trucjes en kan stap voor stap beredeneerd worden, door onder andere in te zien welke symmetrie een parabool bevat.
Vierduizend jaar oude wiskunde
De eerste bekende bron van de abc-formule is vierduizend jaar oud. Toen gebruikte de Babyloniërs deze wiskunde al voor berekeningen met betrekking tot hun landbouwgrond. Ook de oude Griekse, Chinese en Indiase wiskundigen hielden zich bezig met deze formule. Toch bleek de nieuwe, eenvoudige afleiding ervan nergens in de oude wiskundige geschriften terug te vinden.
Po-Shen Loh, die het artikel over de nieuwe afleiding publiceerde, schrijft hoe hij in in historische, wiskundige literatuur de belangrijke stappen voor de afleiding kan vinden. ‘De afleiding had dus honderden jaren geleden al bedacht kunnen zijn. Maar ik kon de complete afleiding nergens terugvinden’, schrijft hij.
Loh werkt aan wiskunde-educatie en -popularisatie. Hij kwam tot de afleiding toen hij wiskundecurricula voor scholieren aan het onderzoeken was. Zijn doel was om nieuwe uitlegmethodes te ontwikkelen.
Gerardo Soto y Koelemeijer, wiskundedocent, postdoc-onderzoeker op gebied van wiskundeonderwijs en schrijver, vindt de methode ‘heel inzichtelijk en korter dan het oplossen door het zogeheten kwadraat afsplitsen‘. Maar de manier waarop hij gepresenteerd wordt, lijkt hij wat overdreven te vinden. ‘Ik heb het artikel bekeken en ben niet echt onder de indruk. Het is niet nieuw of wereldschokkend’, zegt hij.
De abc-formule
En dan nu de wiskunde, voor de liefhebbers. Met de abc-formule kun je de nulpunten vinden van de kwadratische vergelijkingen. De nulpunten zijn de punten waar y = 0. Oftewel, waar de grafiek van y = ax2 + bx + c de horizontale x-as snijdt en waar geldt ax2 + bx + c = 0.
Als je wilt vinden bij welke waarde van x de nulpunten liggen, dan vul je a, b en c in de abc-formule in:
Die los je een keer op voor -b + √(b2 – 4ac) en een keer voor -b – √(b2 – 4ac). Zo vind je de waarden voor x die je zocht. Niet ingewikkeld, wel veel werk. Bovendien moet je die rottige abc-formule onthouden.
De inzichtelijke afleiding
Loh’s afleiding begint met een stap die vaker wordt gemaakt. Je kunt a wegdelen uit de formule. Dat levert op: (a/a)x2+(b’/a)x+(c’/a)= 0/a.
Voor het gemak schrijven we dat als: x2 + bx + c = 0, waarbij de nieuwe b en c de oude (b’ en c’) gedeeld door a zijn.
Nu kun je dit opschrijven als:
x2 + bx + c = (x-R)(x-S) = 0.
Door de haakjes weg te werken kun je zien dat R*S = c en R+S = – b.
Met een voorbeeld:
x2 – 8x + 12 = 0
(x-R)(x-S) = 0
Nu leren scholieren vaak dat ze kunnen gokken welke getallen R en S zijn om ervoor te zorgen dat ze vermenigvuldigd 12 zijn en opgeteld 8.
Loh pakt het anders aan. ‘Als de som van de getallen 8 is, is het gemiddelde 4. En ze liggen beide even ver (u) van dat gemiddelde vandaan’, legt hij uit in een video. Dus: R en S zijn respectievelijk 4 – u en 4 + u. En omdat R * S = 12, krijg je:
16 – u2 = 12
u2 = 4
u = +2 of -2
Vul nu u in om R en S te vinden:
R = 2 en S = 6.
Ten slotte kun je daarmee gemakkelijk de nulpunten vinden via (x-R)(x-S) = (x-2)(x-6) = 0, namelijk x = 2 en x = 6. Zonder te hoeven gokken of een formule uit je hoofd te leren.