Met wiskunde wordt het leven van alledag een stuk gemakkelijker, zo leert het boek Rijk worden met wiskunde. Met relatief simpele optimalisatietechnieken kun je als ware huis-tuin-en-keuken-econoom je opbrengsten al snel maximaliseren. Zo krijg je meer buit voor je duit!

‘Voor niets gaat de zon op’. Dat gezegde herinnert ons eraan dat alles een prijs heeft, al hebben mensen de sterke neiging om te blijven zoeken naar wat ze maar gratis kunnen krijgen. Een kleine industrie vol goeroes en zelfhelpboeken voedt die behoefte, maar de waarheid blijft dat de meeste dingen die de moeite van het hebben waard zijn ook de moeite van het betalen waard zijn, hetzij met geld of door een investering van tijd en moeite. Iedereen die een bedrijf heeft gehad of een groot project heeft uitgevoerd, weet dat er concessies moeten worden gemaakt. Hoe meer er op het spel staat, des te ingewikkelder de dingen worden. De vraag luidt niet of een bepaalde concessie de moeite waard is, maar eerder: wat is de beste concessie die in deze situatie kan worden gemaakt?
Jongleren met factoren
Wiskunde speelt een cruciale rol bij het beantwoorden van die vraag. De dilemma’s waarop we stuiten, vereisen het jongleren met een groot aantal uiteenlopende factoren: tijd, mensen, geld en andere middelen. Bij het zoeken naar het optimale mengsel in een bepaalde situatie proberen we vaak iets te maximaliseren. De productie van een fabriek, het aantal gasten in een restaurant, de beschikbaarheid van verplegend personeel in een ziekenhuis. In andere scenario’s kunnen we zijn gedreven door een noodzaak tot minimaliseren – de koolstofvoetafdruk van een zakelijke reiziger, de kosten van defensie, het budget voor schoolmaaltijden.

Nobelprijswinnaar Anne L’Huillier: 'Het duurde 14 jaar voordat ons idee slaagde'
We spraken Nobelprijswinnaar Anne L’Huillier over haar grootste ontdekking en over haar huidige werk.
Een miljoen andere voorbeelden kunnen worden genoemd. Wat ze gemeen hebben, is dat wiskundigen ze zien als optimaliseringsproblemen, waarvan de bestudering de afgelopen eeuw een van de belangrijkste praktische toepassingen van de wiskunde vormt. Het zijn geen eenvoudige problemen omdat er altijd beperkingen zijn, grenzen opgelegd door beperkte tijd of bronnen of door wezenlijke eisen waaraan moet worden voldaan. Het is duidelijk dat het minimaliseren van het kantinebudget door het dagelijks serveren van enkel patat of het maximaliseren van het aantal gasten in een restaurant door het verwijderen van alle tafels en stoelen zodat iedereen staande moet eten, beide gedoemd zijn te falen.
De uitdaging is dus het optimaliseren van een hoeveelheid, gegeven de relevante randvoorwaarden. De meest populaire benadering van dergelijke problemen is ontwikkeld in de jaren veertig, met name door Leonid Kantorovitsj en George Dantzig, en staat bekend als lineair programmeren. Deze benaming stamt uit de tijd voordat ‘programmeren’ een synoniem voor computerwetenschap werd en in deze context herbergt het meer de betekenis van een ‘programma’ zoals een schema of een tijdstabel. Niettemin ontwikkelde het optimaliseringsonderzoek zich gelijktijdig met de opkomst van de programmeerbare computer. Samen vervullen ze een sleutelrol in het vermogen van de mensheid om ingewikkelde logistieke problemen op te lossen.
Optimaliseer je aardvarken
We kunnen het algemene idee illustreren met een productievoorbeeld, zoals een speelgoedfabriek die twee typen pluchen speelgoed produceert: aardvarkens, voor het avontuurlijke kind, en beren, voor de meer conservatieve klanten. We stellen ons voor dat het bedrijf dagelijks honderdmaal A aardvarkens en honderdmaal B beren fabriceert. Het bedrijf moet bepalen op welke waarden van A en B het moet mikken. Het allereerste dat moet worden bepaald, voor optimaliseringsdoeleinden, is hoeveel de twee speelgoedjes waard zijn. Als ze voor dezelfde prijs in de winkel liggen, moet de fabriek proberen het getal A + B te maximaliseren, het totale aantal dagelijks geproduceerde speelgoedjes (in honderdtallen): een centrale kwantiteit die de doelfunctie wordt genoemd. (Als een aardvarken voor tweemaal zoveel als een beer wordt verkocht, wordt de passende doelfunctie 2A + B).
De benodigde middelen voor het maken van de twee speelgoedjes zijn ook belangrijk. We kunnen aannemen, voor het gemak, dat elk speelgoedje in twee stappen wordt gemaakt. Allereerst moet het worden gestikt met een naaimachine en dan worden gevuld met een vulmachine. Omdat ze qua vorm verschillen, vereisen die taken verschillende hoeveelheden tijd. We nemen aan dat het stikken van honderd aardvarkens 1 uur kost, en het vullen 2 uur. Honderd beren vereisen 3 uur voor het stikken en 1 uur voor het vullen. We moeten nu ook de beschikbaarheid van de machines laten meewegen, bijvoorbeeld 9 uur per dag voor de naaimachine, maar 8 uur (omdat instellen en bijvullen langer duurt) voor de mechanische vulmachine.
Wiskundig gezien is de totale benodigde tijd voor het stikken van A maal honderd aardvarkens en B maal honderd beren gelijk aan A + 3 × B. Aangezien er slechts negen uur beschikbaar is, mag die hoeveelheid niet meer dan negen bedragen. Dat levert ons de eerste randvoorwaarde: A + 3B ≤ 9. We krijgen een vergelijkbare uitdrukking voor de vulmachine, en dat geeft ons als tweede randvoorwaarde: 2A + B ≤ 8. Daarnaast zijn er nog twee nogal voor de hand liggende randvoorwaarden, namelijk dat zowel A als B minimaal 0 zijn, uitgedrukt als A ≥ 0 en B ≥ 0.
Basale vraag
Op dat punt aangeland, bevinden we ons in de juiste positie om een antwoord te geven op een basale vraag: wat zijn de best mogelijke waarden van A en B gegeven deze randvoorwaarden? Dat leidt tot de constatering die het gehele onderwerp smaak geeft, want het antwoord kan het beste meetkundig worden gegeven. De mogelijke waarden van A kunnen worden aangegeven langs een horizontale as en die van B langs een verticale as, waardoor een grafiek ontstaat waarin de coördinaten van elk punt van het vlak overeenkomen met een paar waarden (A, B). Natuurlijk voldoen niet alle paren aan de randvoorwaarden die we hebben gevonden, dus de vraag luidt: welke doen dat wel?
Allereerst zorgen de triviale randvoorwaarden – de minimale productie van nul speelgoedjes, ofwel A ≥ 0 en B ≥ 0 – ervoor dat we ons alleen hoeven bezig te houden met het kwadrant rechtsboven in de grafiek. Alles links van de verticale as (waar A negatief is) en onder de horizontale as (waar B negatief is) kunnen we negeren. De andere randvoorwaarden zijn iets subtieler. De grens voor de naaimachine is wanneer A + 3B = 9. Het belangrijke meetkundige gegeven hier is dat dit een rechte lijn voorstelt. Punten links en onder de lijn (zoals A = 3, B = 1) voldoen aan de randvoorwaarde, en punten erboven en rechts ervan (zoals A = 1, B = 3) niet. Hetzelfde gaat op voor de randvoorwaarde van de vulmachine, met als relevante rechte lijn 2A + B = 8.
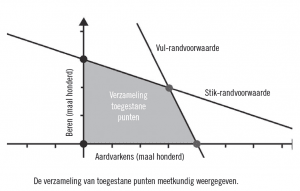
Het intekenen van de lijnen die overeenkomen met de randvoorwaarden levert een vorm op die wordt aangeduid met ‘verzameling van toegestane punten’ ofwel het toegelaten gebied. Dat gebied voldoet aan alle randvoorwaarden. Elke punt in het gebied komt overeen met een paar waarden van A en B die de fabriek in een dag kan produceren. Dat geeft nog niet het antwoord op de vraag wat optimaal is. Het punt A = 0, B = 0 behoort immers ook tot deze verzameling, en dat komt overeen met een fabriek die stilligt. Het beantwoordt echter wel de net zo belangrijke vraag van wat er werkelijk mogelijk is.
Recht en niet krom
Wat opvalt, is dat alle lijnen hier recht zijn in plaats van krommen. Dat is het lineaire deel van lineair programmeren. Dat weerspiegelt het feit dat al de hoeveelheden waarmee we te maken hebben, voortkomen uit het bij elkaar optellen van A’s en B’s. Daarmee hebben we niet-lineaire uitdrukkingen zoals A2 en A × B vermeden. In de echte wereld komt er natuurlijk volop niet-lineariteit voor, en dat maakt het des te meer opmerkelijk – en handig – dat lineaire benaderingen voor de grote meerderheid aan optimaliseringsproblemen volstaan. (Als ze dat niet doen, biedt het meer ingewikkelde vakgebied van niet-lineair programmeren andere technieken.)
De meetkunde van mogelijke verzamelingen vormt het centrale gereedschap voor optimalisering. In ons speelgoedfabriekvoorbeeld is het gebied begrensd. Dat is goed nieuws (hoewel dat niet altijd het geval is) omdat het ons ervan verzekert dat er een oplossing voor het probleem is. Een ander basisgegeven bij lineair programmeren is dat het toegestane gebied altijd convex zal zijn, wat inhoudt dat er geen gaten of inhammen zijn. Formeel gesteld: bij het verbinden van twee willekeurige punten in de verzameling met een rechte lijn, zal het gehele lijnstuk zich binnen het toegestane gebied bevinden en niet daarbuiten. Dat is nog meer goed nieuws, aangezien convexe verzamelingen meetkundig veel gemakkelijker kunnen worden gehanteerd dan hun niet-convexe verwanten.
Meetkundig klinkt dat allemaal prettig hanteerbaar, maar hoeveel dichter zijn we onze doelen voor speelgoedproductie nu genaderd? De sleutel tot het geheel is dat de hoeken waar de randen van de vorm bij elkaar komen, bekendstaan als de extreme punten van de verzameling. Het eerste werkelijk nuttige feit van lineair programmeren is dat de optimale waarde – als die bestaat – altijd verschijnt op een van de extreme punten. Dat maakt het leven onmetelijk eenvoudiger omdat het toegestane gebied oneindig veel punten bevat, maar een eindig aantal hoeken heeft. Voor onze beren en aardvarkens zijn er maar vier, op (0,0), (0,3), (4,0) en (3,2). Om het probleem op te lossen hoeven we nu enkel na te gaan welk van die hoekpunten de maximale waarde voor A + B oplevert. De hoekpunten geven waarden van 0, 3, 4 en 5, dus de oplossing van het probleem ligt op het punt A = 3, B = 2. Het is met deze toewijzing van middelen dat de fabriek zijn opbrengsten zal maximaliseren, met de vervaardiging van in totaal 500 speelgoedjes per dag.
Rijk worden met wiskunde
Het voorbeeld hierboven is natuurlijk nogal eenvoudig, gekozen om de basisideeën van lineair programmeren over te brengen. In het boek Rijk worden met wiskunde lees je nog veel meer praktische toepassingen van de wiskunde. Zo leer je hoe wiskunde je een betere leugenaar kan maken, welke wiskunde schuilt achter digitale fotografie en welke wiskunde Google gebruikt om zijn zoekmachine te optimaliseren. Bestel Rijk worden met wiskunde nu in onze webshop.
Altijd op de hoogte blijven van het laatste wetenschapsnieuws? Meld je nu aan voor de New Scientist nieuwsbrief.
Lees verder:
