In de wiskunde heeft oneindigheid allerlei paradoxale eigenschappen. Hier zie je hoe een som met oneindig veel getallen een eindige uitkomst kan hebben, en hoe ogenschijnlijk kleine getallen samen toch oneindig groot kunnen worden.
De oude Grieken staan bekend om hun briljante wiskunde. Maar met hun voorkeur voor exacte getallen en geometrische weergaven hadden ze nogal moeite met het begrip oneindigheid. Dat leidde tot de ‘paradoxen van Zeno’, waarvan de race tussen Achilles en de schildpad de beroemdste is.
In dat gedachte-experiment neemt de snelvoetige Achilles het in een hardloopwedstrijd op tegen een schildpad. De schildpad krijgt een kleine voorsprong. Achilles heeft die achterstand vrij snel overbrugd, maar in de tijd die hij daarvoor nodig had, is de schildpad alweer een stukje verder. Zodra Achilles die afstand heeft overbrugd, is de schildpad weer ietsje verder. En zo gaat het maar door.
Dit is hoe we wiskundefobie te lijf kunnen gaan
Sarah Hart vertelt hoe we de angst voor getallen en formules weg kunnen nemen.
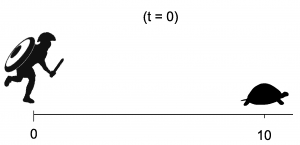
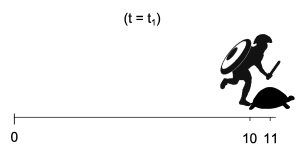
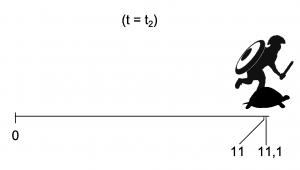
Achilles moet dus oneindig veel afstanden overbruggen om de schilpad in te halen. Dat gaat hem nooit lukken. Of toch wel?
Oneindige som
De denkfout bij deze paradox is dat je ervan uitgaat dat oneindig veel stukjes bij elkaar altijd leiden tot een oneindig lange weg, waar Achilles oneindig lang over doet. Dat is niet zo; in dit geval is de oneindige som van alle afstandjes wel een eindig getal.
Stel bijvoorbeeld dat de afstand tussen Achilles en de schildpad bij aanvang één meter is, en dat de Griekse strijder twee keer zo snel loopt als de schildpad. Dat betekent dat de afstand telkens gehalveerd is wanneer Achilles een stuk heeft overbrugd. Alles bij elkaar moet Achilles dan 1 + 1/2 + 1/4 + 1/8 + 1/16 + … meter inhalen. Je voelt het misschien al op je klompen aan: dat is in totaal 2 meter. Daar heeft Achilles niet lang voor nodig – zeker niet oneindig lang.
Van oneindig naar 23
Hier hebben we dus een som van oneindig veel getallen die uiteindelijk toch een eindig getal oplevert. Dat heet een ‘convergente reeks’. Wanneer een reeks wel naar oneindig gaat, is hij divergent. Een voorbeeld daarvan is de harmonische reeks:
1/2 + 1/3 + 1/4 + 1/5 + 1/6 + … = ∞
De som loopt vrij langzaam op; na honderd termen ben je nog maar net boven de vijf. Toch zit er geen limiet aan deze reeks. Als een schildpad kruipt hij verder en verder omhoog, tot in het oneindige.
Het grappige is dat je deze divergente reeks met slechts een kleine ingreep convergent kunt maken. Haal bijvoorbeeld alle termen weg waar het cijfer 9 in zit. Je zou zeggen dat dit weinig uitmaakt, aangezien de termen met een 9 aan het begin van de reeks nauwelijks iets toevoegen. Toch is de reeks nu hartstikke convergent: de som is iets minder dan 23. We zijn van oneindig tot onder de 23 gezakt! Ook als je een ander cijfer of een willekeurige combinatie van cijfers uit de reeks weghaalt, wordt hij convergent.
Hardlopers zijn doodlopers
Twee eindige getallen zijn samen nooit oneindig. Dat betekent dat de termen die we uit de harmonische reeks hebben weggehaald, samen wel oneindig groot moeten zijn. De som van alle breuken waar een 9 in zit is dus divergent:
1/9 + 1/19 + 1/29 + … + 1/89 + 1/90 + 1/91 + … = ∞
Hoe kan deze som oneindig veel groter zijn dan de som met alle cijfers behalve 9? Dat komt doordat er verderop in de harmonische reeks, wanneer de getallen steeds langer worden, veel meer termen met een 9 zijn dan zonder. Daardoor krijgen ze toch de overhand – een beetje alsof de schildpad Achilles alsnog terugpakt.
